The following interactive simulations were programmed with the java-akin language Processing (www.processing.org).
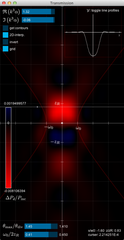
Parhelic Circle Intensity Distribution Simulator (interactive)

This real-time interactive simulation provides the intensity distribution and colouring of the Parhelic Circle (PHC) halo. This allows comparison to artificial halos created by illuminating a spinning hexagonal prism or to natural halos at very low solar elevations and thick plate-oriented displays only. Use the right panel to change the index of refraction of the hexagon material. Water ice has an approximate index of 1.31, whereas BK7 glass has an index of refraction of 1.51-1.53 (red to blue wavelength). The effect of a finite light-source elevation can also be included. This script only considers in-plane ray paths, i.e. no paths which enter or exit through the top and bottom basal crystal faces!
For more information about the Parhelic circle and associated parhelia, see the webpage of Les Cowley.
The left plot shows the result for ice. Clearly visible is the Liljequist Parhelion around 153° and the Sundog (22° Parhelia) at around 22°.
The computation uses the concept of effective intercepted areas which are redirected into a certain azimuthal angular range. For each ray path (48 paths are considered) the following product determines the amount dI of (unpolarized) light that is redirected into a particular direction. Each index (m) corresponds to an individual ray path entering one of three entrance faces for prism orientations in the range [0,30°]. Several such paths can be grouped into a single category, i.e. ray paths of type 3-7 (sundogs) etc.

The simulation data can be exported as a CSV file with the following structure:
(0) sum of all ray paths (no obstruction), (1) 3-7 (22°PH), (2) 3-5-7-3 (90°PH), (3) 3-8-7-5 and 3-5-6-7 (LQPH2), (4) 3-5-6-7-3 (LQPH1, RT#1), (5) 3-7-5, 3-8-7, (6) round-trips (excluding those visible with obstruction), (7) 3-7-4, (8) 3-6-4, (9) 3-5-7-4 and (10) 3-6-8-4 (120°-PH), (11) 3 (external reflection), (12) total intensity for obstruction exp., (13) round trips visible with obstruction (RT#2, RT#3, ...), (14) 3-6-3, (15) 1-3-2, (16) 3-8-7-5-3, (17) theta [rad], (18) theta [°deg]
The simulator looks the following way:

A small bug report: Please press "i" in order to get the correct 132 path intensity distribution. For an up-to-date version please email me.
321 ray path

The simulator includes the 132 ray path responsible for most of the PHC intensity at non-zero solar elevation. The geometrical constraints were only attempted in approximation. For each prism orientation, the top face (1-face) surface area available to a certain 1-3-2 path is determined. This effective area, in combination with the Fresnel factors, determines the amount of light redirected into a certain direction, and thereby the intensity in this azimuthal domain.
Computation according to the following sketch and expressions:
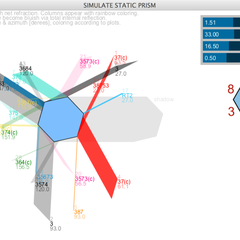
Static Prism Illumination
The parhelia circle intensity distribution tool relies on the computation of 43 individual ray paths entering 3 possible side faces for prism orientations in the range 0°-30°. The following
tool visualises the exiting columns / beams of light under parallel illumination and a static prism of fixed (variable) orientation. Each column represents a particular ray path, notated
using the system of the book of Walter tape. The addition of the string "(c)" indicates that the path includes net-refraction and appears rainbow-colored (dispersed). The program uses the
effective areas as column widths and the Fresnel coefs (unpolarized) as transparencies to give an approximate impression of the appearance to be expected for any orientation and light source
elevation. The positions of the exiting beams within the exiting faces are not accurate since this information is not required for the PHC intensity distribution computation.
Nonetheless, this tool helps to identify the emerging light columns in a photograph.
Transmission (Interference) Microscopy Scans

Implementation of the theory published in "Energy-Redistribution
Signitarures in Transmission microscopy of Rayleigh and Mie particles", Journal of the Optical Society of America
A (JOSA A), Vol. 31, No. 11, pp 2370-2384, M. Selmke and F. Cichos, 2014
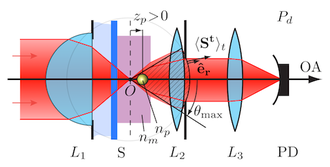
This processing script visualizes the predictions of the generalized Lorenz-Mie theory concering the relative transmission signal ΔP(x,z)/P in a scanning sample microscopy setup for a small Rayleigh particle. Herein, x and z denote the lateral and axial offset of the particle relative to the incident Gaussian beam's focus. Small means that the size-parameter x=kR should be smaller about wavelength/20. Using the Clausius-Mosotti relation one may then compute for a given particle-size, its refractive index and the wavelength used the complex-valued polarizability. This quantity determines the transmission signal in combination with two setup-parameters: The focusing parameter s (the ratio of the beam waist to the Rayleigh-range) and the ratio of the collection angle to the beam's angle of divergence (theta_max/(2*s)).
The application uses 48 pre-computed dats-sets of 21x31 pixels (x/w0=0..4, z/2zR=0...3) for selected combinations of setup-parameter (10 collection angle ratios: {0.01, 0.21, 0.41, 0.61, 0.81, 1.01, 1.21, 1.41, 1.61, 1.81} and 11 focusing parameters: {0.05, 0.075, 0.1, 0.125, 0.15, 0.175, 0.2, 0.225, 0.25, 0.275, 0.3}) using n=150 multipoles. The complex-valued polarizability α = Re(α) -i Im(α) changes their relative weight. The exact polarizability may be obtained from the first Mie coefficient, while a the value corresponding to a radiative reaction corrected Clausius-Mosotti polarizability provides an easily computed approximate expression.
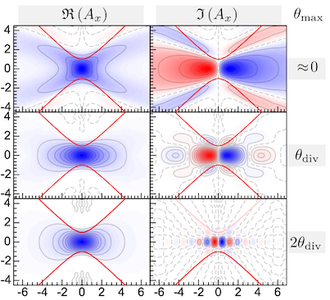
The relative transmission signal is the change in collected transmission normalized to the background. It may be either positive (blue), indicating an enhanced transmission due to the corresponding placement of the Rayleigh-particle in the focal region, or the signal may be negative (red), indicating a reduced / diminished transmission for that position.
- Large negative imaginary parts of the particle's polarizability α result in a large absorption and therefore in n enhanced weighting of a dip-like and negative component. This component grows and saturates when the collection angle exceeds the beams angle of divergence (the collection angle ratio becomes larger than 1).
- Large positive real parts of the particle's polarizability α result in a dispersive signal shape, indicating the energy-redistribution. Also, for large collection angles this component disappears in magnitude. The scattering contribution which would then dominate (for small but non-negligible x) is neglected here. The neglect is justified for x<0.1 up to collection angle ratios of about 2.
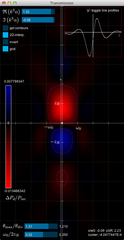
The 2D-bilinear interpolation (http://en.wikipedia.org/wiki/Bilinear_interpolation) of the used data-sets is the default. In this setting, contours may be displayed statically, i.e. by pressing "Do Contours".
If the 2D-bilinear interpolation may be turned off to display the original data, i.e. the spatial sampling of the data set of Ax.
For the proccesing source code only: The script requires an installation of the blobDetection library and the ControlP5 library.
Program shortcuts:
- "b": draw beam-waist on/off
- "g": grid on/off
- "x": plot x-axis and z-axis on/off
- "i": 2D-interpolate on/off
- "p": switch through profile mode (x,z,none)
The processing script requires an installation of the blob-detection library (http://www.v3ga.net/processing/BlobDetection/)

The following scripts have been written for Mathematica (http://www.wolfram.com).
Mathematica scripts for confocal transmission microscopy, light-particle interaction near-fields & photothermal detection

These Mathematica script files allow the extensive study of scattering phenomena enountered in coherent focused beam illumination of spherical (multilayered) scatterers, e.g. to compute the intensity collected by a detection microscope objective and recorded with a Photo-Diode. The extensive theory can be found in the supplement of the ACS article "Photothermal Single Particle Microscopy: Detection of a Nano-Lens" and free in the supplement of the early ArXiv-version (see published papers). The Gaussian on-axis modeling which the scripts cover mostly is also described in the Optics Express article "Nano-lens diffraction around a single heated nano-particle".

The code allows for the individual inspection of the constituting parts of the photothermal signal, i.e. the scatter flux and the interference flux encountered in the artificial total-field decomposition in the generalized Lorenz-Mie theory.
Interestingly, the PT signal (red line) is only linear in the heating power of both the scattering (blue) and the interference (black) contributions are considered in sum.

The off-axis BSCs allow the calculation of recorded scatter images, i.e. scans of nano-particles (NPs) across the focal region of a focused laser beam from which the transmitted intensity is recorded on a photodiode. Thes exemplary images to the left can be found in the article "Gaussian beam photothermal single particle microscopy" Fig. 4 where they were compared to actual measurements. The ability to compute these images allows for the extraction of the actual NP porition inside an optical trap for instance. While for resonant beams (see green image) the dip in the recorded scatter-image closely follows the laser-particle offset, the off-resonant (red image) image shows a dispersive structure with the NP being in the focus halfway in the dispersive structure.
Such calculations also allow an extraction of the beam's waist size from a measured scatter image. Nanoscopic beam profiling and PSF mapping with ultrastable metallic nanoparticles hereby becomes feasable.

The scripts also allow the investigation of the near field, i.e. the structure of the local electromagnetic field and Poynting vector flux lines in the direct vincinity of nano and microspheres under plane wave and even shaped beam illumination. Hereby, phenomena such as "photonic jets" can be studied which occur for transparent microspheres illuminated by light, see the article by Kofler et al. or the thesis by S. Lecler. Also, the resonant energy uptake (absorption) by metallic nanoparticles, such as AuNPs under 532nm illumination, may hereby be studied.
Computation Examples: GaussGLMT_Examples_RadPressure.nb, GaussGLMT_Examples_FarField_Photothermal.nb, GaussGLMT_Examples_NearField.nb
Dieletric constant vs. wavelengh for Gold: au_diel.txt

The following interactive simulations were programmed with the java-akin language Processing (www.processing.org).
All simulations use pre-rendered images and illustrate the physics and phenomenology of photothermal microscopy, the photothermal lensing effect and hot Brownian motion.
Bird Flocking

Based on a bird-flocking model devised by Prof. Matthew Truner from the physics department of the British Warwick University (http://homepages.warwick.ac.uk/~phscz/) and presented on the diffusion fundamentals conference 2013, this processing script implements a natural bird-flocking algorithm. Each individual of the swarm / flock updates its velocity direction according to a weighted sum of a local average (of the 4 nearest visible neighbors), a random term and a term based on the projection of the flock as seen from the bird.
The following article of M. Turner's group gives further details:
The Role of Projection in the Control of Bird Flocks, D. J. G. Pearce, A. M. Miller, G. Rowlands and M. S. Turner, Proc. Nat. Acad. Sci., 111, 10422 (2014).
Photonic Rutherford Scattering Simulator

This interactive simulation allows the user to view the effect of a refractive index gradient on a incident beam of light as predicted by Fermat's least optical path priciple. For a given refractive index profile (blue plot) a ray of light will propagate in such a way as to minimize its optical path and will thereby bend towards the medium with higher refractive index. This principle is also the explanation for the mirage effect which can be seen above hot asphalt where at grazing view angle a reflection can be observed.
The simulator allows the changing of the refractive index profile n(r)=(dn/dT)*DT*R/r by two sliders. A convergent lensing or a divergent lensing may be adjusted by changing the sign of the thermorefractive index (dn/dT), and the amplitude of the refractive index perturbation is simulated by the slider which controls the AuNP temperature (red plot). A single ray or many rays may be visualized. For the single ray its asymptotes are shown. The cut with the optical axis defines the focal length assiciated with the lensing. If many rays are shown, they will follow an adjustable gaussian intensity distribution.
A warped checkerboard/net/quads texture may also be displayed by the appropriate checkboxes in the bottom right corner. It reproduces an experiment where a siple checkerboard texture is imaged through the n(r) profile medium.
Interactive Photothermal Microscopy Simulator
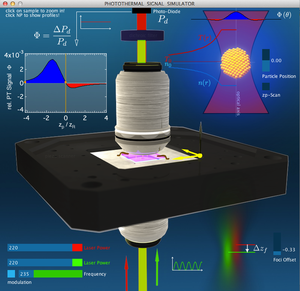
Shown are the key parts of a typical photothermal confocal microscopy setup: A piezo scanner (black) which can move the sample (purple, blue) which is fixed to it in lateral and axial directions, the heatingand the detection laser, the two microscope objectives and the transmission detecting photo-diode. For a detailed account see published papers (ACSNano article).
The axial coordinate can be controlled by the particle position slider in the top right corner. Moving the piezo stage has the effect of moving a particle in the sample relative to the fixed focused beams (red and green). A continuous particle position scan can be done by clicking the checkbox.
The laser powers can be adjusted in the bottom left corner. The green heating laser can be modulated with the modulation checkbox above and the modulation frequency may be adjusted. The green heating laser can further be offset relative to the probing beam (controller and illustration in the bottom left).
The resulting PT signal (red/blue) is plotted in the top left corner, while its angular distribution is shown in the very top right corner. Here, also the probe-beam modification is illustrated. The temperature and refractive index profiles around the particle may be shown by clicking on the big particle.
Interactive Hot Brownian Motion Simulator & Photon Nudging

This interactive simulator shows a random diffusion process for a gold-nanoparticle which is heated in the shown green laser focus, i.e. hot Brownian motion (see published papers).
The particle may be dragged to the central region where it is heated and will experience enhanced diffusion, or it may be dragged to a region in which it will not be heated by the laser and will thus perform normal Brownian motion. The temperature and viscosity profiles around the AuNP can be displayed and illustrate the fact that they are quasi-instantaneously carried along with the AuNP (since heat diffsion is very fast on nm length-scales).
Also shown are the time-trace of the rel. PT signal detection volume and the signal as it would be recorded with a photothermal microscope (see working principle above), the induced particle temperature and the instantaneous hot Brownian Diffusion coefficient and the efective HBM temperatures for rotational and translational diffusion.

The same tool allows the visualization of Photon-Nudging developed in by co-workers and in cooperation with the Haw Yang lab in Princton. See article: "Harnessing Thermal Fluctuations for Purposeful Activities: The Manipulation of Single Micro-swimmers by Adaptive Photon Nudging", Chemical Science, 2012, Qian, B., Montiel, D., Bregulla, A., Cichos, F. and Yang, H.
The bottom right panel allows to activate "Photon Nudging" via a toggle. Then, manual photon nudging is availiable upon pressing the enter-key. If furthermore the "target"-option is activated, a target may be specified with the mouse to which the automatic nudging tries to navigate the particle to. Above these toggles, the active swimmer's velocity and the acceptance angle for automatic steering may be set. One may also set an external magnetic field (B-field) to harmonically fix the janus particle's orientation for manual steering. The field-direction is adjustable with a slider or the arrow-keys. The strength of the field determines how well the particle will be aligned against thermal fluctuations.
Also, changing the particle radius changes the ratio of translational to rotational motion. Not showing the particle image (deactivate Particle toggle) but only the trajectory runs the simulation faster.
Raindrop / Rainbow simulator
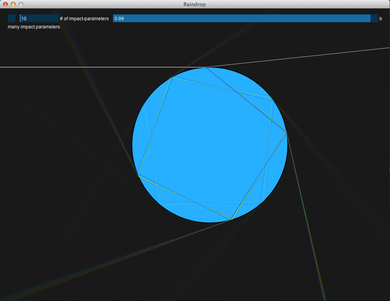
This interactive sketch simulates the refraction and dispersion of a beam of white light by a spherical water-droplet.
One may drag and move the drop and manually change the impact-parameter by clicking into the sketch. Alternatively, the impact-parameter can be fine-adjusted between 0.95*R and 1.0*R with the slider (top). Also, one may change to the homogeneous one-sided illumination mode (checkbox in the top left corner) where the formation of a rainbow is visualized!
Capped Sphere

An interactive simulation of the (multiple) reflections and refractions occuring in a sphere (or a cylinder) which is capped by a reflective coating of variable angular extent. Also, the photonic forces may be calculated for a cylinder from a homogeneous illumination in this 2D approximation. The forces are indicated by arrows and a graph may be plotted.
Macular Degeneration Analyzer and Reverse Distortion
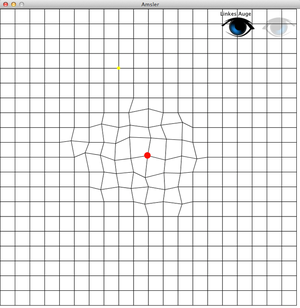
Macular Degeneration is a disease where the retina's morphology is distorted. This causes the patient to have a distorted vision. Usually, this distortion is only significant around the focus. The Amsler grid can visualize and analyze this distortion. A regular grid is perceived by a healthy person simply as a regular. A patient with macular degeneration, however, will perceive a distorted grid. The patient is then asked to keep focusing on the central red dot while movoing the vertices of the grid around such that he finally perceives an undistorted regular grid. A healthy person will now see a distorted grid (see image) which shows the distortion of a perfectly regular grid as seen by the patient. The distortion information quantified in this manner may then be used to morph an image such that it will appear undistorted to the patient!
This is exactly what the tool presented here can do.
Further references: http://www.opt.indiana.edu/riley/HomePage/Amsler_Grid/4TEXTamsler_grid.html
The tool is based on ideas presented by Walter Kohn on the Lindau Nobel Laureates Meeting of 2012 (http://web.physics.ucsb.edu/~kohn/)
Miscellaneous
Maya Platonic Solid constructor
Excel Elements (VBA-based interactive Excel periodic table of elements and more)